Archive for the ‘MathEdZine’ Category
- There are 4 quarts to a gallon, 2 pints to a quart, and 16 ounces to a pint. There are 4 ounces to a gill. There are (about) 26.4 gallons in a hectoliter. How many gills are in a hectoliter? Display the unit fractions for your calculation.
- Write as a single number in scientific notation: ( 1.5 * 10^{-17} ) / ( 7.5 * 10^8 ).
3. Consider sets X, Y, and Z in a universal set U, where
U = {b, i, g, f, a, t, c, o, d, e}
X = {e, g, b, d, f}
Y = {f, a, c, e}
Z = {b, e, a, t}.
Use the operations \prime, \cap, \cup—complement, intersection, and union—to find the sets represented by the given expressions.
X \cap Y = { f, e}
Y \cup Z =
Z’ =
(Y \cup Z)’ =
(X \cap Y) \cup Z’ =
X \cap (Y \cup Z)’ =
4. Sum the sequence: 88 + 99 +110 + . . . + 462.
5. Expand the expression (x-3)^4.
6. 250 beverages are tested for Purity, Body, and Flavor.
65 pass the Purity test.
95 pass the Body test.
90 pass the Flavor test.
20 pass on both Purity and Body.
25 pass on both Purity and Flavor.
40 pass on both Body and Flavor.
5 pass all three of the tests.
How many of the beverages pass *none* of the tests?

starting with the mathy stuff
on what used to be a door
(
at the corner of what used to
be a street: in “the livingston
library”, or, more precisely,
as i think of it, at the living-
ston “branch of the UUCE” libe,
where for “UUCE”, read th’
UU church in reynoldsburg
[ohio; do i have to tell you
*everything*?]… g-d willing
i might make it back to the
*main* branch while it still
stands…):
a bunch of taped-up drawings (and
reproductions of same) by me.
the entire RHS (right-hand side,
natch) is given to various versions
of “desargues’ theorem in color”;
there’s another of these at upper-
-left (& in between, “vlorbik’s
seven-color theorem” [in one of its
many versions]).
then the three big (eight-&-a-half-by-
-eleven) 16-point thingums; these are
versions of the “hurwitz tesseract”
(as i hereby dub it); the two 8-point
“cosets” of the normal 8-group in the
unit integral quaternions. a-four-hat,
as i like to call it. anyway.
and, illegible here more or less of course,
the back cover of an em-ed-zed (M Ed Z —
“math ed zine” to the acronym-averse).
featured here are *more* covers of MEdZ
(what else?): specifically, this very one
(#1—the “hip pocket vocab”, 2010; reissued
in digest size with new [-ly reprinted]
graphics & hand-lettered comments [same year,
i think]); K_n -slash- K_4 (a “remix” of
two “microzines” [eight pages on one side
of an 8 1/2 by 11 each] into one such);
P_2(Z_2) & P_2(F_n) (“projective planes”);
& ,
, &
(“number sets”).
but enough about me. some of my *other* stuff.
r.~crumb’s _art_&_beauty_ (cover shot of mrs.~
~crumb). two “books” with comic-book-swearing
for “titles”; also clowes’ _modern_cartoonist_.
that poster of magazine covers from _starlog_.
you could look at that thing alone for quite
a while. in the right company. (alas.)
what you can’t see covering up part of this
poster (lower left) is the _comic_book_artist_
cover by i-know-not-who showing “magnus
robot fighter” clobbering an evil droid. i did
a song about fighting robots and have a soft
spot for this character.
two pics of fitzgerald & a bunch of his books; you
might also be able to see burroughs. in the brick
under the pez-head of winnie-der-pooh is a period
shot of dad early 60s. you can tell the images
of auden are *there* in my version but not who
they are images of; likewise langston hughes.
this is quite a satisfying way of making the time
go by as long as you don’t wish for somebody else
actually to *read* it…

… but really it’s the *same* d-mn thing,
over and over.
i can now say for sure that some of the drawings
in these old Math Ed Zines scattered all around
the place could be adapted for coloring books.
the B&W drawing underlying both colorations
is from a zine of about ten years ago and shows
graphically (“lectures without words”) that
. you’d see this code
on the actual display if i could get a decent
shot. a poor workman blames his tools. and i
intend to make the most of it.

from blank file-folder (and no idea)
to conceived, drafted, penciled, and inked
before finishing my third cup of coffee:
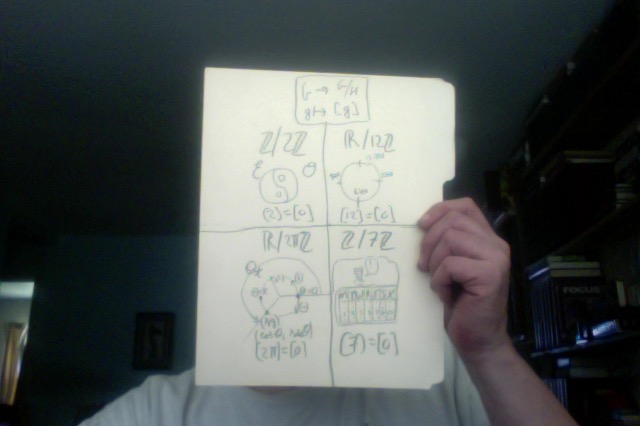
behold: MEdZ # (1+i+j+k)/2!—
th’ G-mod-H issue!! in which we can see
no less than *four* (count ’em) more-or-less
familiar examples of “modding by a subgroup”.
namely,
(-+) {E,O}—even & odd: the ol’ cosmic yin-yang…
(++) time considered as an endless spiral of half-days…
(- -) the “unit circle” & the “periodic functions”…
(+-) time considered as an endless spiral of weeks.
one can easily look up the (- -) diagram expanded
at arbitrary length in textbooks considering “trig”.
and the helices of endless time are too familiar
to say much more about. the “clock face”, though,
is a bottomless well of shorthand examples—there’s
a car trying to run us off the road at three o’clock—
and so might be worth some further development
if it were useful in, say, fixing notations.
but (-+) one is prepared to go on about at any length.
is one of the most useful finite sets there is,
after all. for example, the 64 hexagrams of the i-ching
amount at some level to displayed pleasingly.
in the zine by me about “the 64 things” the hexagrams are
replaced with “subgraphs of K_4” (where of course K_4 is
the “complete graph on four points”; a diagram having
six edges [giving the six “lines” of the ching in that
version]; the 64 things are then subsets-a-six-set
[say {y, b, r, p, o, g} for the “full color” version]).
for example. i hope to continue in this vein later.
hello out there. ☰☱☲☳☴☵☶☷

the seven black triangles are
the blends
Mud Yellow Purple
Mud Red Green
Mud Blue Orange
the blurs
Yellow Blue Green
Yellow Red Orange
Blue Red Purple
and
the ideal
Purple Orange Green.
the “theorem” in question is then that
when the “colors” MRBGPYO are arranged
symmetrically (in this order) around a circle
(the “vertices”of a “heptagon”, if you wanna
go all technical), these Color Triples will
each form a 1-2-4 triangle.
but wait a minute, there, vlorb. what the devil
is a 1-2-4 triangle. well, as shown on the “ideal”
triple (center bottom), the angles formed by these
triangles have the ratios 1:2:4. stay after class
if you wanna hear about the law of sines.
note here that a 1-4-2 triangle is another beast altogether.
handedness counts. (but only to ten… sorry about that.)
anyhow, then you can do group theory. fano plane.
th’ simple group of order 168. stuff like that.
all well known before i came and tried to take
the credit for the coloring-book approach.
with, so far anyway, no priority disputes.
okay then.
the tetrahedral group at left: A_4, to the group-theory geeks.
up top, the “yrb” labeling of the vertices of a cube,
with the bit-string digital code and a 2-D projection.
the seven-color theorem… concerning the simple group
of order 168 & MRBGPYO… is hinted at.
under that, as one can *kind of* read on the blurry photo,
is “desargues theorem in color” — ten “points”
(one Mud, two Yellow, two Blue, two Red, one Green,
one Purple, one Orange) in abstract “space”.
the best version… i’m not technically up to drawing it…
is to put the colors on the ten diagonals of a dodecahedron.
next best is the five-point star version taking up
the biggest part of the file-folder.
next to that on the right: the vertices of the cube
colorized again. pretty much the same way if memory serves.
the points-to-lines “duality” is colorized better here, i think.
at the bottom, several versions of the seven-point star version
of the MRBGPYO theorem… and other stuff about heptagons.
there’re some books in there, too. that’s it for today.

here one has labeled the vertices of a cube
with (“euclidean”) 3-space co-ordinates.
the “origin”… we can think of it as
our “point of view”… is at 000.
[the “point” in 3-space usually
denoted (x, y, z) is here written
as “xyz”; we restrict our attention
to the values in {0, 1} for these
variables (since the (8) points
000, 001, 010, 011,
100, 101, 110, 111
then form the vertices of our cube).]
putting the primary colors (Red, Yellow, & Blue)
“on the x, y, & z axes (respectively)”, i.e., putting
Red—>001
Yel—>010
Blu—>100,
we may then conveniently put the *secondaries*
(Green, Orange, & Purple) at the “third vertex” of
the back left wall (“G = Y + B”),
the front left wall (“P = R + B”), and
the floor (“O = R + Y”)
(respectively).
the last vertex is the “ideal” point 111;
all the colors blend here to form Mud.
cool algebra ensues. but not till after dinner.
or you could look it up.
here’s a hex board
with seven icons on it;
each icon has seven colors;
the seven permutations of
colors-into-hexes (each icon
has seven hexes) can be
considered as the objects
of a cyclic group.
specifically
{
() = \identity
(1234567) = \psi
(1357246)= \psi^2
(1473625)=\psi^3
(1526374)=\psi^4
(1642753)=\psi^5
(1765432)=\psi^6
}.
(of course one has \psi^7=\identity,
etcetera… the group here is
essentially just integers-mod-7:
{ [0], [1], [2], [3], [4], [5], [6]},
with addition defined by
“cancelling away” multiples
of 7 (forget about the fancily
denoted “permutation structure”
displayed in defining \phi
and just look at the exponents).
the “cycle notation” used here
is *much* under-used, in my opinion.
but we’ll really only need it
for future slides.
my latest… i thought i was quarterly
when i issued it but maybe i’m semi-annual…
looks like this.
1876
2345
in the upper left are the “covers”:
these become the front and back
of the zine in folded form.
i discussed the title a few hours ago
(along with some other stuff).
suffice it to say here that our
subject is self-dual spaces.
*under* the title (in folded form;
above it here) are two
representations of the *simplest*
example: duality in P^2(F_2).
the space P^2(F_2) is itself
displayed (without a duality)
on p.5 (the lower right of the
photo) in the usual “triangle” way.
the colors are used to show
how these two objects…
*and* a certain subobject
of the space on pp. 7 & 8
(the 21-point P^2(F_4))…
can be considered “the same”.
the lower left (pp. 2 & 3)
are the desargues configuration.
i’ve discussed it recently
(here, for example)
and’m starting to hurry.
finally then (for now),
the cube-and-cross sections
bits are much the most vivid
visual motivator i’ve found
for the concept of “projectivity”.
the colors are surprisingly
helpful here. i’ll try to convince
you later. company coming. bye.
introductory ramble
i’ve been passing around the “spring 2011”
issue of MEdZ pretty freely and’ve posted
quite a bit *about* it.
but it isn’t very well-organized.
so in hopes of finding a curious reader
hoping to learn about the pictures in the zine
(MEdZ S’11 is in pictures-only “lecures
without words” format… an 8-page
micro-zine “unstaplebook” made by copying
all 8 images [including the front & back
covers of course] onto a single standard sheet
and cut-and-folded into tiny-booklet form;
this is the first issue in color and very much
my personal favorite [of the moment]), i decided
to poke around in the ol’ Archive for the ‘Graphics’ Category
(and so on) and write out some connecting remarks.
prehistory of MEdZ S ’11
the title is .
i pronounce this “ess is isomorphic
to the dual of ess” if i read it
symbol-for-symbol; one might also
read it (more freely) as
“S is a self-dual space”.
in some sense, this zine is about
spaces isomorphic to their own duals.
whatever that might mean.
in Some Finite Projective Spaces (01/07/11)
are several lectures-without-words shots
from earlier zines. including this one:
.
this was something of a breakthrough drawing for me.
(Self-duality of the Fano Plane, one might call it
[were it not a lecture-without-words].)
somehow i’d finally stumbled on a “visual” representation
for duality. this inspired a great deal of graphical
fiddling around by me. the same algebraic tricks
used in constructing the 7-point-to-7-line duality
for fano space could *also* be used on any n-point “space”
having n = 1 + q + q^2,
where “q” is some power-of-a-prime.
fano space is the case q = 2. so i did q=3 and q=5
(and the results are in the post i’ve linked to above)
and published ’em. by february 1, i’d developed
a much cleaner-looking graphical presentation
for these (projecive-planes-of-small-order).
but the next real “breakthrough” ideas
came with the case of q=4. in this early draft
i went a little bit “deliberately weird looking”.
a later version of Self-duality of the Projective
Plane Over the Field of Four Elements
became the last display of the (black-and-white)
edition of Spring 2011 and i announced it
on april 17.
but now i have to backtrack. i haven’t done any of the math.
okay. enough for today.
PS. fall quarter finds me doing two sections
of Calc !V at big-state-u. i met the lecturer
wednesday and met my students thursday. whee!




