binary tetr’al | the livingston review

Archive for the ‘binary tetr’al’ Category

as easy as i know how

September 11, 2020 in binary tetr'al

Photo on 9-11-20 at 8.49 AM

so here’s the thing i’ve been in the process

of memorizing ever since i worked it out.

i *almost* know it now. this interface sucks.

bye now.

the same old thing

June 22, 2020 in binary tetr'al, Graphics, Zines

here’s yet another version of this thing
(which, like all its predecessors, is unreadable
in the version posted here; don’t get me started):
four “representations” of the 24-element group
called variously “the binary tetrahedral group”,
“the hurwitz units”, SL_2(F_3), and A-four-hat
(among other things).

new here are the yin-yangs on the g-coset points
of the generators-and-relators version at upper left.
and nothing else. still, it’s an entire course
in group theory summarized on one page and it cost me
quite a bit of effort figuring out what to put where.
maybe some of the bits-into-graphics pages of my book
were as much trouble as this but i doubt it. anyhow,
i’ve long since given up on ever again getting anybody
to read *that* damn thing so i’m stuck with this until
i find a better obsession. read the ten page news.

Photo on 6-22-20 at 3.03 PM

teach your children

June 18, 2020 in binary tetr'al, TeX

here it is in code.

$ii = \begin{pmatrix} \begin{pmatrix} 0 & 2 \\ 1 & 2\end{pmatrix}& \begin{pmatrix} 1 & 1 \\ 0 & 1\end{pmatrix}& \\ \begin{pmatrix} 1 & 0 \\ 2 & 1\end{pmatrix}& \begin{pmatrix} 2 & 2 \\ 1 & 0\end{pmatrix} \end{pmatrix}$
$i = \begin{pmatrix} \begin{pmatrix} 1 & 2 \\ 1 & 0\end{pmatrix}& \begin{pmatrix} 2 & 1 \\ 0 & 2\end{pmatrix}& \\ \begin{pmatrix} 2 & 0 \\ 2 & 2\end{pmatrix}& \begin{pmatrix} 0 & 2 \\ 1 & 1\end{pmatrix} \end{pmatrix}$

$iii = \begin{pmatrix} \begin{pmatrix} 0 & 1 \\ 2 & 2\end{pmatrix}& \begin{pmatrix} 1 & 0 \\ 1 & 1\end{pmatrix}& \\ \begin{pmatrix} 1 & 2 \\ 0 & 1\end{pmatrix}& \begin{pmatrix} 2 & 1 \\ 2 & 0\end{pmatrix} \end{pmatrix}$
$iv = \begin{pmatrix} \begin{pmatrix} 1 & 1 \\ 2 & 0\end{pmatrix}& \begin{pmatrix} 2 & 0 \\ 1 & 2\end{pmatrix}& \\ \begin{pmatrix} 2 & 2 \\ 0 & 2\end{pmatrix}& \begin{pmatrix} 0 & 1 \\ 2 & 1\end{pmatrix} \end{pmatrix}$

$II= \begin{pmatrix} (mgy) (nrp) & (ybr) (pog) & \\ (mro) (ngb) & (mpb) (nyo) \end{pmatrix}$
$I= \begin{pmatrix} (bo) (mpgnyr) & (mn) (ygbpro) & \\ (yp) (mbrnog)& (rg) (mopnby) \end{pmatrix}$
$III = \begin{pmatrix} (mbp) (nor) & (mor) (nbg) & \\ (yrb) (pgo) & (myg) (npr) \end{pmatrix}$
$IV = \begin{pmatrix} (rg)(mybnpo) & (yp)(mgonrb) & \\ (mn)(yorpbg) & (bo) (mryngp) \end{pmatrix}$

$jj= \begin{pmatrix} hk & g & \\ gk & hi \end{pmatrix}$
$j= \begin{pmatrix} -gi & h & \\ -hj & -gj \end{pmatrix}$
$jjj = \begin{pmatrix} gj & hj & \\ -h & gi \end{pmatrix}$
$jw = \begin{pmatrix} -hi & -gh & \\ -g & -hk \end{pmatrix}$

back-of-the-envelope calculations

June 17, 2020 in binary tetr'al, Finite Geometry

Photo on 6-17-20 at 8.05 PM

here’s A-four-hat three ways.

but really *four* ways; like we agreed upthread,
the trit-string version is inherent in the very
positioning of the table entries, to wit.
consider
-+___++
– -___+-
—the “quadrants” of beginning algebra…
iterate: each of the three “versions” of our group
has each of its entries in one of the (16) “positions”
-+-+___-+++___++-+___++++
-+- -___-++-___++- -___+++-
– – -+___- -++___+- -+___+-++
– – – -___- -+-___+- – -___+-+-
; now just remember that, e.g.
“+- -+” in this context means
(1-i-j+k)/2—a “hurwitz unit”
in $\Bbb{H}$ —the quaternions
(or, if you prefer… as i do… in
$\Bbb{Z}[h,i,j,k]$ —the *integral*
quaternions). where was i.

the matrix notation is “mod 3”;
the generators-and-relators version
requires one to work with “relators”
like “hi = jh”—(this is, like, the
very *textbook example* of a
“semi-direct product”, if you want
my opinion… anyhow, this is quite
close to the actual way *i* actually
got it if i can be said to have it now]).

finally, the “permutation notation” version
is very much the easiest to work with (and you
should learn right away how to work with these
if you haven’t already; i had to be dragged
slowly and painfully into accepting this stuff
but maybe you’ll be one of the lucky one in
a million): one readily sees which elements
have order six, for example.

anyhow, this is one of the coolest things i ever
put on one sheet of paper or so it seems to me now.

what profiteth a man to flee his fate?

June 16, 2020 in binary tetr'al, Notations

let
$B =\begin{pmatrix} \begin{pmatrix} \begin{pmatrix} 0 & 2 \\ 1 & 2\end{pmatrix}& \begin{pmatrix} 1 & 1 \\ 0 & 1\end{pmatrix}& \\ \begin{pmatrix} 1 & 0 \\ 2 & 1\end{pmatrix}& \begin{pmatrix} 2 & 2 \\ 1 & 0\end{pmatrix} \end{pmatrix} & \begin{pmatrix} \begin{pmatrix} 1 & 2 \\ 1 & 0\end{pmatrix}& \begin{pmatrix} 2 & 1 \\ 0 & 2\end{pmatrix}& \\ \begin{pmatrix} 2 & 0 \\ 2 & 2\end{pmatrix}& \begin{pmatrix} 0 & 2 \\ 1 & 1\end{pmatrix} \end{pmatrix} \\ \begin{pmatrix} \begin{pmatrix} 0 & 1 \\ 2 & 2\end{pmatrix}& \begin{pmatrix} 1 & 0 \\ 1 & 1\end{pmatrix}& \\ \begin{pmatrix} 1 & 2 \\ 0 & 1\end{pmatrix}& \begin{pmatrix} 2 & 1 \\ 2 & 0\end{pmatrix} \end{pmatrix} & \begin{pmatrix} \begin{pmatrix} 1 & 1 \\ 2 & 0\end{pmatrix}& \begin{pmatrix} 2 & 0 \\ 1 & 2\end{pmatrix}& \\ \begin{pmatrix} 2 & 2 \\ 0 & 2\end{pmatrix}& \begin{pmatrix} 0 & 1 \\ 2 & 1\end{pmatrix} \end{pmatrix} \end{pmatrix}$

now let
$B=\begin{pmatrix} II & I\\ III & IV\end{pmatrix}$ , i.e., let
$II = \begin{pmatrix} \begin{pmatrix} 0 & 2 \\ 1 & 2\end{pmatrix}& \begin{pmatrix} 1 & 1 \\ 0 & 1\end{pmatrix}& \\ \begin{pmatrix} 1 & 0 \\ 2 & 1\end{pmatrix}& \begin{pmatrix} 2 & 2 \\ 1 & 0\end{pmatrix} \end{pmatrix}$ , etc., so that
I, II, III, and IV (the “quadrants”) denote
two-by-twos of two-by-twos.

we’ll call the smallest matrices in sight “points”.
e.g.,
$h =\begin{pmatrix} 2 & 1 \\ 0 & 2\end{pmatrix}$ ;
the quadrants are now two-by-two arrays of “points”.

on the graphical models i’ve been going on about all week
the quadrants are (respectively)
I ++
II -+
III —
IV +-
(as is familiar to every calculus student);
expanding on the same logic gives the “trit-code”
for the individual points. for example,
h = ++++
and so on.
one then simply translates the 16 trit-strings
++++, +++-, ++-+, … —-
into “hurwitz units” like
$h = {{1+i+j+k}\over2}$ ;
voila.

oh, yeah. i forgot to say. the “points” are
matrices *mod 3* (so that 2 = -1). that is all.

his dark materials

June 14, 2020 in binary tetr'al

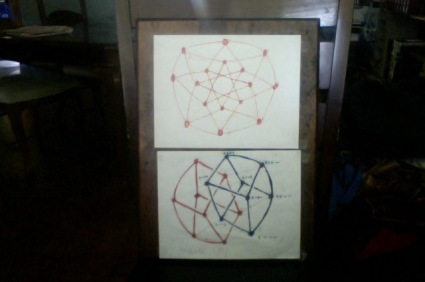
the monochrome dots-and-lines thingum up top is copied
from a by-hand copy of an online graphics-giz. jpg or
pdf or i dunno what. fuggedaboudit. point is,
the two-tone diagram underneath has the *same* 16 points…
one might almost imagine that one point-set had literally
been *traced* from another… but now there are two
distorto-cubes: a blue & an orange. i’ve filled in
the “trit-string” representation of a projection of
the “h-coset” (the blue “cube”); the orange is the
negative of this one so you can easily fill in
the trits if you should so desire. or could if
you could see the damn things on the blue. anyhow,
point is, i had to *fill in* those co-ordinates
(
h := ++++, g:= h^2 = -+++, … hi, gi… gk…-h=—-:
the sixteen points of the “tesseract” obtained
by shifting the “fundamental quaternion units”
[eight of ’em] to the “right” and “left”
[the “past” & the “future” on another convenient
model].
)
and “connect the dots” literally to see how the
doggone monochrome was a picture of a tesseract at all.
that’s the way i roll. staring at the diagram…
however pleasant.. just wasn’t gonna get it.

and i am reminded of a remark of mine in some blog
or another long ago: the student isn’t learning
if the pencil isn’t moving (the eraser counts).

Photo on 6-14-20 at 1.49 PM

as i was saying

June 10, 2020 in binary tetr'al

/*
the (so-called) fundamental quaternion units
can be represented as
$\pm 1 =\pm\begin{pmatrix} 1&0\\0&1\end{pmatrix}, \pm i =\pm\begin{pmatrix} 0&1\\2&0\end{pmatrix}$
$\pm j =\pm\begin{pmatrix} 1&1\\1&2\end{pmatrix}, \pm k =\pm\begin{pmatrix} 1&2\\2&2\end{pmatrix},$

with the scalars of the matrices considered
as elements of $\Bbb{F}_3$ —i.e., 2=-1 etc.
*/

now let
$h =\begin{pmatrix}2&1\\0&2\end{pmatrix},$
—the “h” is for hurwitz; let g = h^2
(remember everybody is mod-3; i’d better
get that in somewhere if i’m actually
gonna bring *calculations* into play…)
then \pm (that’s plus-or-minus for you
TeX newbies)
1, i, j, k,
h, hi, hj, hk,
g, gi, gj, gk
is HU—or A-four-hat—or $SL_2(\Bbb{F}_3)$ —
or what have you. the binary tetrahedral group.

before you throw anything away, zap it so you’ll have a copy

June 9, 2020 in binary tetr'al

here’s the other image of a-hat from w’edia.

this one looks quite a bit more like the diagrams
i’ve been drawing in pursuit of a geometric “feeling”
for—what i’ve been calling—the “binary tetrahedral”
group; what i’ll be calling “a-hat” ( $\hat A$ —this rhymes
with “A-flat”, not “the cat”) henceforth. this is
short for a-four-hat. the idea here (as i found
on some webpage) is that our group
is a “covering” of A_4—th’ “tetrahedral group”
aka the “alternating group on four objects”.

(
the four objects in question, in the unlikely
event that anyone is following so far, “are” the
vertices of the tetrahedron in question…
the group
A_4 = { (),(01)(23),(02)(13),(03)(12),
(012),(021),(013),(031),(023),(032), (123), (132 }
(typing is fun and easy)…
then is made to represent the three 180-degree
“flips” and the eight 120-degree “rotations”
that permute the vertices of a tetr’on [while
preserving its “orientation”—if we allow for
reversals we get the cube-group S_4].
the vertices i call up, down, equal & opp.
in the “covering”, they become the color-pairs
mud-neuter yellow-purple, blue-orange, & red-green.
get it?
)

perhaps this will refresh your memory

June 8, 2020 in binary tetr'al

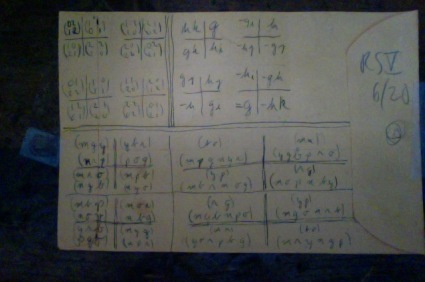
here on the front of one big envelope are
four versions of the “binary tetrahedral group”:
HU-code,, permos, generators, & matrices.
taken together they form “the BT rosetta stone”.
i posted a bigger version a few days ago.

there’s a semester’s worth of algebra in that display.
i know because it took me much longer than that
to figure out how to do it.

Photo on 6-8-20 at 7.03 PM

the same old thing

June 7, 2020 in binary tetr'al, Graphics

here’s HU—the hurwitz units, aka
BT the binary tetrahedral and also
$SL_2( \Bbb{F}_3)$ the 2-D special linear group
for the field of order three… not to mention
the “permutation” representation…—
graphically with pro production-values.
i haven’t groked the layout yet.
800px-Binary_tetrahedral_group_elements