Message: I Care
I’d been groping for the right notation for Transformations of Graphs since the first day; I settled it over the weekend.
By I will mean a certain Transformation of the xy-plane (at this point I tend to write “
” on the board; of course
, but none of this “set-theoretical” language has made it into my lectures so far). To wit:
.
This definition obviously takes the “maps to” notation () for defining functions for granted—which I’ve sort of been doing all along without pinning myself down with anything as vulgar as a definition. The right-hand side of the latest equation, then … hold it. Does everybody know that the colon-equalsign
combination means “equals by definition”? Well, it’s a pretty handy little trick, let me tell you. OK. Now. The RHS in our latest equation expoits a notation rarely seen in lower-division texts (alas): instead of the ungainly “Let f be the function defined by “, we have the straightforward declaration
(“eff, by definition, is the function that maps ex to ex-squared”).
The more familiar notation gives a “formula” not for itself but for
. A lot of people would have you believe that this distinction doesn’t matter and in certain contexts such people must even be put up with. But it sure matters to me, here and now. Because once I know how to write definitions in the “maps to” style, I don’t need to mention any arbitrary old letter-of-the-alphabet like f when what I’m really talking about is “the squaring function” … and I can just go ahead and write down facts like
: this is calling things by their right names (“The inverse of the function mapping x to the cube root of x–plus-five is the function mapping x to x–cubed, minus five”—you just can’t write that sentence in “f(x)” style … only something like “Let f be BLAHBLAH; then f-inverse is LALALA”— but what’s any of it really got to do with anything called “eff”?).
Readers already familiar with all of these ideas—or astonishingly quick on the uptake—might notice that, so far, it might appear that I don’t actually need the “maps to” notation for my purposes.After all (for example), one has (recall that a function is a set of ordered pairs)—and the “ordered pair” version is almost as concise as the “mapping” language. But here’s the real payoff: the “arrow” notation carries over seamlessly when the domain is, say,
(ordered pairs of numbers as opposed to individual real numbers)—and this is the application we actually wanted:
denotes the “reflect in the y-axis” transformation. Note that
is harder to scan (anyway, so it seems to me); also
invokes that pesky “T” and anyhow you try getting students to believe that
simply won’t do as a LHS.
So. Whenever we say “reflect in the y-axis”, we can write . And I’ve been saying so all along. What’s new here is that I’m proposing to call it
. This has the drawback that it “freezes” the variables x and y: wherever “angle brackets” are in effect, x and y must mean “the first and second co-ordinates of a certain ordered pair” (note that, by contrast,
; the variable names here can be changed without changing the actual set of orderded pairs itself).
And this “freezing” is indeed somewhat unfortunate. But I’m more than willing to pay that price, to have a quick-and-dirty way to spell “shift left by three”: is sure as heck gonna be a lot easier to calculate with.
-
1
Pingback on Sep 22nd, 2020 at 4:12 pm
[…] Some Math piecewise functions01/22/09 Big Day For Former Math Professor self-publishing01/22/09 Message: I Care notation for transformations01/23/09 It’s Not The Cheat, It’s The Futility needless […]
-
2
Pingback on Dec 14th, 2020 at 12:59 pm
[…] Some Math piecewise functions 01/22/09 Big Day For Former Math Professor self-publishing 01/22/09 Message: I Care notation for transformations 01/23/09 It’s Not The Cheat, It’s The Futility needless […]
January 22, 2009 at 3:30 pm
I like it, especially your notation for reflections.
I confess though I’ve always been unhappy with the -1 superscript standing for both “the inverse” and “raised to the exponent -1”.
January 22, 2009 at 5:01 pm
thanks!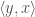 , natch)…
, natch)…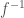 one had, say,
one had, say,  .
. symbol …). delicate issues
symbol …). delicate issues
speaking of inversion
(
i’ve wished aloud in earlier versions
of the class (and elsewhere) that instead
of
but now i’m not so sure. i’m planning on having
the angle-bracket-transforms compose
from left to right (because this is how
the drawings go in the text, e.g.), but the text (rightly)
presents function composition using (the standard)
right-to-left composition (of real valued functions
of a real variable; i’m not *exactly* introducing
a clash in the notations … still i’d better not use
the
arise pretty much as soon as you start this process;
you can’t always be sure which direction the “arrow”
should point …
the locus classicus of the

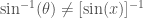 .
.
“overused -1 superscript” might be
the ghastly notation clash whereby
but
i mean really. come on. one can’t have been serious.
November 24, 2010 at 8:09 pm
f=[x|—->y] has become rather a hobbyhorse for me…
as i only realize now in presenting “inverse functions”
again for the first time since winter 09. it’s just
*way* better and everybody should start doing
it my way right now please.
i already knew that “getting the right notations
is crucial (and textbooks are usually the opposite
of helpful)” was a hobbyhorse. so this is some
kind of *sub*-hobbyhorse (taking its place alongside
“don’t write out over and over again what
you’ve already taken the trouble to define
a symbol for” [and many others]).
in other news
especially when the very text sez don’t bother
(as is the case for me right now).
May 13, 2011 at 6:12 pm
jason on notation:
and a test case:
September 12, 2021 at 7:01 am
heh. he said “ordereded”. next-to-last line of next-to-last paragraph.