Why Live
It so happens that . And this, all by itself, far from being a cause for despair, is kind of a cool thing to know. What depresses me more than I can safely say is that “factoring trinomials” is a very big deal around here (I blog out of the office even during breaks because I don’t have the social skills needed to establish an internet connection at home) and that this particular equation very clearly has no place in our curriculum.
So. What then are we to do? Well, first of all, obviously, verify it (take nothing on authority in mathematics). Maybe you’ll notice that the RHS (“right hand side”, natch) can be parsed as ; for me this was the easiest way to check (because the Special Product Formulas of our 103 class are second nature to me; I can do the expansion to
[a “difference of squares”] mentally and mentally use the “square of a binomial” formula to expand further; one
“cancel”s; done). Or not; it’s fun to watch six terms of the longer expansion wipe themselves out. Then what? Well, then ask, “how could I have found this out if I didn’t know it already?”.
And the awful truth there is: Google it. This online rootfinder was pretty easy to find and gave back our result more-or-less correctly (I’m quibbling with some notations and suchlike conventions here; nonexperts needn’t be troubled by my weaselwordage). “Google it” is the right answer to a lot of questions!
No, really. Stick with me here. Lord Satan appears to you and says “Factor x^4+x^2+1 over the integers and I will spare your tribe; fail and I will annihilate you all without appeal.”. What do you do? Well, if you’re good in algebra, you solve it (and check it very carefully); if not, well, if you’ve got any sense, you get up on the internets and find a page that’ll do it for you. The last thing you’d do (if you’ve got any sense) is take our 103 course or anything like it: not only won’t they tell you how to find this out, they’ll probably leave you with the impression that you know for sure that x^4+x^2+1 is prime or something; alas, your very teacher will probably think it’s prime.
So what are we spending so much time and money for, trying to teach these poor devils to do badly what an easily-accessed robot slave can do well? And, assuming for the moment that there are good reasons for doing so, is it at least possible to be honest about it?
Because, check it out: if we rewrite the question as “How could I have found this out without a computer?”, we’ll encounter some interesting math, along with some insights into the Remediation Congame that has replaced Mathematics Education rightly-so-called with its putrefying corpse.
First of all, notice that Lord Satan said we had to factor our polynomial over the integers. But if he’d said “over C” (i.e., over ; this typesetting interface is free but otherwise far from perfect), one would (do I get to say “of course” here?) have a different answer:
, where
. My point here, for now, is simply that the domain over which we are to factor a given polynomial matters: it’s part of the problem and needs to be part of the problem statement (again, assuming we’re interested in trying to be honest). I’m not proposing here that 103 students need to learn about the complex number field before learning about factoring polynomials (and neither do I say that that it’s necessarily a bad idea for them to do so); one could point out that x^2 – 2 is prime over the rationals but
over the reals (and, indeed, seeing that our texts and courses seem determined not to make this point, one is led to wonder how—if at all—they expect to be taken seriously in making such a fuss about the distinction between the reals and the rationals in an earlier part of the course … every chance to actually use the distinction having apparently been rigorously suppressed).
OK. Once we do allow ourselves to mention C, we can make a great deal of progress. It’s probably not wildly optimistic to hope that the median-level students of a 104 class could use the quadratic formula to write down the four complex solutions to , namely
. It probably is wildly optimistic to hope that they could then write down the four roots separately. I’m not kidding. A few “A” students might be able to produce the equation
(which is of course equivalent to the C-factorization I gave earlier). A student that could produce this equation with no other instruction from me than “Factor x^4+x^2+1 over C” would gladden my heart more than I can say even though I don’t approve of square-roots-of-negatives written without the “plus-minus” sign. Bitter experience convinces me that most 104 students, even given the “x=” solution I provided above, couldn’t produce the factored-form equation with me right beside ’em telling ’em how to do it. It’s like they feel themselves physically incapable of writing down anything so messily algebraic. Not that I blame ’em (much); you’ve gotta walk before you run.
OK. But a 148 student could probably do it. Still couldn’t multiply out the result and check it, though: for that we’ll need a better notation. So let and take it from there:
,
, and so on (inscribing a hexagon in the unit circle is helpful here). But we sure as heck don’t do this in 148 around here; it’d take a week. And nobody cares. Not the students, not the publishers, not the department, nobody. Just me.
What am I even supposed to be doing here? Does everybody else involved actually want me to get up in front of the room and say, “Look, in real life you’re going to let the computer take over whenever anything gets at all complicated, so never mind trying to understand the big picture: that’s for the experts anyway, and the creators of this course don’t want you to learn to think like an expert …”? Because I don’t need this god-damn job that bad. I can beg on the street.
-
1
Pingback on Sep 22nd, 2020 at 4:12 pm
[…] Fear And Trembling scheduling; politics12/18/08 Why Live (x^4 + x^2 + 1) tricky factoring12/24/08 Jeremiah 6:14 peace, […]
-
2
Pingback on Dec 14th, 2020 at 12:59 pm
[…] 12/02/08 Fear And Trembling scheduling; politics 12/18/08 Why Live (x^4 + x^2 + 1) tricky factoring 12/24/08 Jeremiah 6:14 peace, […]
December 18, 2008 at 4:28 pm
what you *can* do in 103 — so i do —
or have done — i’m hoping never to do it *again* —
is look at x^6 – 1. this can be considered *either*
as a “difference of cubes” *or* as a “difference of squares”.
x^6 – 1 = (x^2 -1)(x^4+x^2+1)
on the one hand and
x^6 – 1 = (x^3+1)(x^3-1)
on the other. three of the right-hand-factors
factor further (with the same familiar formulas):
x^2 – 1 = (x + 1) (x – 1) [natch],
x^3 + 1 = (x+1)(x^2-x+1),
x^3 – 1 = (x-1)(x^2+x+1);
make the appropriate substitutions;
“cancel” common factors; out pops
x^4 + x^2 + 1 = (x^2 + x +1) (x^2 – x + 1).
part of the point is that this still depends on
stumbling on the result by dumb luck;
it still doesn’t tell us how to factor x^4 + x^2 + 1
*without* “already knowing the answer”.
which, admittedly, neither have i, quite.
the role of the complex cube (and sixth-) roots
of unity was sketched in hastily because i figured
anyone able to follow me thus far
would easily see that it could easily be done …
and that *having* done it, we’d have the
*integer* factorization in hand at long last,
by straight-up follow-your-nose computation.
December 18, 2008 at 8:28 pm
The first thing that came to me was roots of unity, but let me try this as a student:
Substituting q = x^2 and using the quadratic formula quickly gets you in complex-number-land. Doing so shows that *if* x^4+x^2+1 does factor over the integers the factors both have to be quadratic.
Ok, so at most three terms each. The first terms multiply to be x^4 so the quadratics have to start with x^2. The last terms multiply to be 1 so the quadratics have to end with 1. Checking what we have on a table:
x^2 ?*x 1
x^2 x^4 ??? x^2
?*x ??? ??? ???
1 x^2 ??? 1
Clearly one of the x^2 needs to cancel. We need a -x^2 in the middle to do that, so the only way is by using an x and a -x.
So we have our x^2+x+1 and x^2-x+1.
…
Yuck, that felt very brute force and special-case-y. Why are they obsessed with this again?
December 18, 2008 at 8:30 pm
One more try on the table. Needs fixed width really.
— x^2 ?*x 1
x^2 x^4 ??? x^2
?*x ??? ??? ???
–1 x^2 ??? 1
December 18, 2008 at 9:26 pm
After noting that the polynomial has no linear factors, we look for quadratic factors. If a factorization exists then it has the form (x^2+ax+1)(x^2+bx+1) or (x^2+ax-1)(x^2+bx-1). Multiply them out, equate coefficients, and solve for a and b.
December 18, 2008 at 9:26 pm
After noting that the polynomial has no linear factors, we look for quadratic factors. If a factorization exists then it has the form (x^2+ax+1)(x^2+bx+1) or (x^2+ax-1)(x^2+bx-1). Multiply them out, equate coefficients, and solve for a and b.
December 19, 2008 at 5:12 am
Why not just add x^2 and then subtract x^2 to the lefthand side. You have (x^4 +2x^2 +1) -x^2 which you can then factor.
The example you gave of x^6 -1 always occurs in these classes. I suppose it’s easiest to just tell students to factor as the difference of squares first, then cubes. If they reverse the procedure, you’re right–that trinomial can’t be factored by ordinary means. Butthis way there is at least a fairly simple technique for at least demonstrating that you can get the same results either way.
Happy to see you came out of ‘retirement’ and are teaching again. I guess misery loves company.
December 21, 2008 at 4:25 pm
So: why? and with whom?
Because it along the way we run into some fairly interesting mathematics (including, see comments above), and the other stuff you said.
With whom? With anyone who reads your blog, obviously.
In my high school classes I assign 2 chunks of homework: plain practice, with a slightly more challenging core. But students may opt to substitute one or two much more challenging problems for the practice – and a few encounter problems that look like this one… I see that I assigned x^4 + 4a^2 a few weeks ago… Assumes they will use Hypatia’s method (an example, a model, is in the text, and the problem refers them back to it).
That being said, I think there is something delightful about the Anonymous approach.
Finally, I take your admonitions seriously, but in this case, I was already there. We specify at least once what we are factoring over. My fairly strong text falls down on this, which is especially annoying since, in the exercises, they generously supply trinomials which cannot be factored over the integers.
Jonathan
December 22, 2008 at 7:37 pm
thanks to all the commenters; i was well aware
that i was exaggerating my plight in complaining
that “nobody cares” but me; still it’s very nice
to have that confirmed just by looking away
for a weekend and coming back.
i’m still shaky over jason dyer’s improvised notations
but he appears to be saying much the same thing
as anonymous david: this is indeed the most
straightforward approach to learning the key fact
of this post (as presented in the “lord satan” form);
thanks for pointing it out here.
this would’ve been a better post if i hadn’t punked out
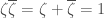
on the roots-of-unity stuff; the role of
is supposed to be a big selling point for the “big picture”
but i left it out almost entirely (i remark that i had
“6” in place of that “3” until an hour ago and hereby
gently chide all my readers for letting me get away
with it for so long).
is eerily reminiscent of “2*2 = 2+2” and simply begs
for further study.
if x^6 – 1 really “always occurs” in 103-equivalent
classes, then i’ve exaggerated far more than i knew.
i’m willing to bet that when i check a few of the texts
in the department library that it won’t even *usually*
occur (even as an exercise). i kind of hope i’m wrong.
jonathan’s last paragraph seems to support me
in mistrusting the texts … it sure doesn’t surprise me
that such an experienced teacher has the habit of
correcting such oversights. much of what i seem
constantly to be complaining of is that this kind of thing
is no *mere* oversight; i believe it’s more-or-less
*designed in* by a process of downdumbing that
repels but fascinates me …
as to “just add and subtract x^2” …
well, sure, i suppose … but isn’t there
a sort of “what would eisenstein do?”
aspect to that? … perfectly obvious
*if* you’ve been fiddling around with
polynomials in an *obsessive* way …
(this is called “getting good” and
comes highly recommended.)
i essentially mentioned this trick
as a technique for *checking* the result;
i’m suggesting in the previous paragraph
that it would be an unusually insightful
student that came up with the “add zero” trick
in the context of “factor x^4 + x^2 + 1”.
December 21, 2010 at 4:17 pm
sue v.’s f is for factoring.
http://rationalexpressions.blogspot.com/2010/12/factoring-resources.html
July 27, 2011 at 2:59 pm
a^4 + 4b^4: sophie germain’s identity.